PeilingPraktijken

Soms krijg je een tip als iemand een foute grafiek langs ziet komen. Voor de grafiek in figuur 1 werd ik getipt door Achim Scholtes (Saxion Hogeschool in Enschede). Ook Casper Albers (Rijksuniversiteit Groningen) schreef er een column over in De Volkskrant. De grafiek toont de gemiddelde lengte van mannen in een aantal landen. Er zijn grote problemen met deze grafiek. Er is van alles mis mee. Je kunt hem bijna niet goed interpreteren. Je wordt op allerlei manieren op het verkeerde been gezet.

De grafiek in figuur 1 is afkomstig van de Engelse website Patient.info. Die website bevat veel informatie over allerlei mogelijke medische onderwerpen. Met de leus “Health information you can trust” presenteert de website zich als een “comprehensive directory of evidence-based clinical information”. Deze website mag dan misschien medische informatie van hoge kwaliteit beloven, met de statistische informatie in figuur 1 is behoorlijk veel mis.

Het eerste probleem betreft de verticale as. De schaalwaarden zijn in feet (voeten) en inches (duimen). Er gaan 12 duimen in een voet, en een duim is 2.54 cm. Deze schaalverdeling mag dan prettig zijn voor de Engelsen, maar voor andere landen is het bijzonder lastig de waarden af te lezen.

Een tweede probleem heeft ook te maken met de verticale as. Die begint niet bij 0, zoals dat wel zou moeten, maar bij vier voet en tien duimen (blijkt na enig gereken). Een consequentie van deze fout is dat de verschillen in lengte van de menselijke figuren veel groter lijken dan ze eigenlijk zouden moeten zijn. Als je alleen naar de lengte van de manlijke figuren kijkt, dan is de Nederlandse man bijna vier keer zo lang als de Indonesische man. Dit is natuurlijk onzin. Een blik op de cijfers leert dat de Nederlander slechts 1,16 keer zo lang is als de Indonesiër (183,8 tegen 158,0).

Een derde ernstig probleem met de grafiek is het gebruik van menselijke figuren. In feite is de grafiek een staafdiagram. Het is daarom beter de figuren te vervangen door staven. Een probleem van de figuren is dat hun omvang niet de waarde van de getoonde variabele (lichaamslengte) weerspiegelt. Als je bijvoorbeeld het oppervlak van de figuren voor Nederland en Indonesië uitrekent, dan blijkt de Nederlander ruim 12 keer zo groot te zijn als de Indonesiër. Dit verschil is dus veel te groot.

Je ziet deze fout wel vaker langskomen bij grafieken waarin symbolen zijn gebruikt. Al in 1983 wees de bekende statisticus Edward Tufte in zijn boek “The Visual Display of Quantitative Information” op de gevaren hiervan. Hij introduceerde zelfs een maat voor de mate waarin een grafiek de waarde van bepaalde verschijnselen verkeerd weergeeft. Dat is de Liegfactor. Die krijg je door de waargenomen waarde in de grafiek te delen door de werkelijk waarde. Bij een goede grafiek is de Liegfactor gelijk aan 1. In de grafiek in figuur 1 is de Nederlandse figuur 12,12 keer zo groot als de Indonesische figuur terwijl de gemiddelde lengte van de Nederlandse man 183,8 / 158,0 = 1,16 keer zo groot is als de gemiddelde lengte van de Indonesische man. De Liegfactor is dus gelijk aan 12,12 / 1,16 = 10,45. Dit betekent dat de verschillen in de grafiek een factor 10 te groot zijn. Er klopt dus niets van de verhoudingen in de grafiek.

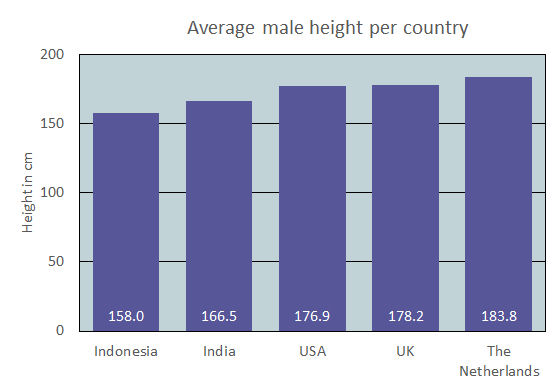
De eenvoudigste manier om problemen met de omvang van symbolen te vermijden, is helemaal geen symbolen te gebruiken, maar gewoon een simpel staafdiagram. Dat gaan we in twee stappen doen. In de eerste stap maken we van de grafiek in figuur 1 een staafdiagram met verticale staven. Dat leidt tot figuur 2. In de tweede stap draaien we het staafdiagram 90 graden, zodat we een staafdiagram met horizontale staven krijgen. Dat levert figuur 3 op. In figuur 2 zijn dezelfde gegevens gebruikt als in figuur 1. De verticale as is gerepareerd. Hij begint nu bij 0 (zoals het hoort). En voor de schaalwaarden is overgegaan van voeten en duimen op meters en centimeters.

De figuren zijn vervangen door blauwe staven. Die staven zijn allemaal even dik. Dus de hoogte van de staven weerspiegelt de gemiddelde lengte van de mannen in de verschillende landen. Merk op dat de lichaamslengtes in figuur 2 veel minder variëren dan die in figuur 1. Indonesische mannen zijn inderdaad nog steeds het kleinst (en Nederlandse mannen het grootst), maar de verschillen zijn veel kleiner.

Omdat de staven los van elkaar staan hoeven ze niet per se verschillende kleuren te krijgen. Je kunt de verschillende staven uitstekend van elkaar onderscheiden als ze dezelfde kleur hebben. Hier is gekozen voor de kleur blauw. Nog een andere verbetering is dat horizontale roosterlijnen zijn toegevoegd. Die helpen bij het aflezen van waarden uit de grafiek.

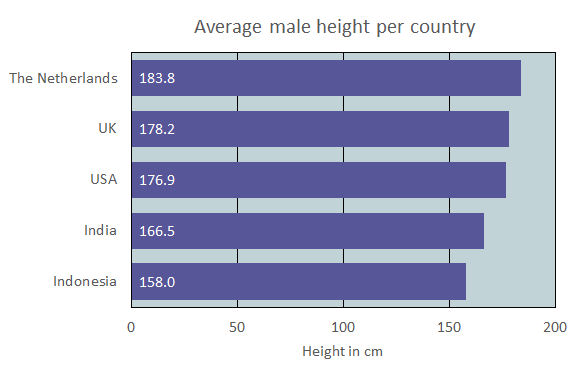
Als een staafdiagram veel staven bevat dan kan het gebeuren dat er te weinig ruimte is voor teksten onder de staven. Dat zie je al een beetje gebeuren in figuur 2. Je kunt dan een kleiner font gebruiken voor de tekst, of de tekst uitsmeren over meer regels. Dit bevordert de afleesbaarheid echter niet. In deze situatie is het wellicht beter om de grafiek te draaien en horizontale staven te gebruiken. Dat is gebeurt in figuur 3.

De informatie in figuur 3 is dezelfde als in figuur 2. Er is nu voldoende ruimte voor de namen van de verschillende landen. Ook hier begin de as bij 0. En roosterlijnen helpen bij het aflezen van waarden in de grafiek.

We kunnen concluderen dat de staafdiagrammen in figuren 2 en 3 en stuk beter zijn dan de grafiek in figuur 1. Ze geven een eerlijker beeld van de lengteverschillen in de vijf landen. Gebruik van een grafiek als in figuur 1 moet heel sterk worden afgeraden. Het is een foute grafiek.